Tot nu toe hebben we het vooral gehad over het vermogen van onze menselijke motor. We hebben gezien dat ons vermogen bepaald wordt door de 4 energieprocessen in onze spieren. Doordat de verhouding van de 4 energieprocessen verandert met de tijd, neemt ons vermogen af naarmate we de inspanning langer moeten volhouden, zoals de formule van Riegel laat zien. We weten ook dat het anaerobe drempel vermogen (de ADV in Watt/kg) de beste maatstaf is voor ons prestatievermogen en dat deze overeenkomt met het vermogen dat we gedurende 1 uur kunnen volhouden. Tenslotte hebben we aangetoond dat de grenzen van het menselijk prestatievermogen ongeveer liggen bij een ADV van 6,4 Watt/kg voor mannen en 5,7 Watt/kg voor vrouwen.Nu komen we aan de vraag hoe we kunnen berekenen hoe snel we kunnen fietsen met een bepaald vermogen? Daarvoor moeten we kijken naar de natuurkunde van het fietsen: wat zijn de weerstanden die we moeten overwinnen? In de evenwichtssituatie (dus zonder versnellingen en vertragingen) zijn dat er 4:1. De rolweerstand (van de banden en het wegdek).2. De luchtweerstand (ten gevolge van de wind en onze eigen snelheid)3. De klimweerstand (tegen heuvels en in de bergen).4. De mechanische weerstand (van de ketting en de naven).In de evenwichtssituatie moet het vermogen van onze menselijke motor precies gelijk zijn aan de som van de benodigde vermogens om de 4 weerstanden te overwinnen. We gaan daarom eerst deze 4 weerstanden nader analyseren.
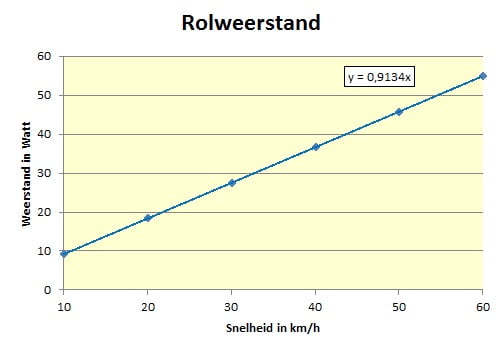
RolweerstandHet benodigde vermogen (in Watt) om de rolweerstand te overwinnen is afhankelijk van de rolweerstandsfactor cr, het gewicht m (in kg) en de snelheid v (in m/s), zoals in de box weergegeven.

Het voorbeeld is weer voor snelle Eddy, die 75 kg weegt en een fiets heeft van 8,8 kg. Zijn ADV is 4 Watt/kg, dus in totaal kan hij 4*75 = 300 Watt trappen. Bij een snelheid van 40 km/h is het aandeel van de rolweerstand in zijn totale vermogen dus 36,5/300 = 12,1%. In de grafiek zien we dat de rolweerstand van Snelle Eddy in de praktijk kan variëren van 10-55 Watt.In deel II gaan we nader in op alle factoren die de rolweerstand bepalen en het effect daarvan op de haalbare snelheid.Voor de volledigheid melden we hier nog even dat strikt genomen in de bovenstaande formule nog een factor cos(boogtan(i/100)) moet worden toegevoegd, waarbij i het hellingspercentage is. In de praktijk is deze factor nagenoeg gelijk aan 1 (zelfs bij een helling van 20% is hij maar 0,98). We hebben hem dus in de box maar weggelaten, in onze calculatoren op www.hetgeheimvanwielrennen.nl hebben we hem uiteraard wel meegenomen.
 Luchtweerstand
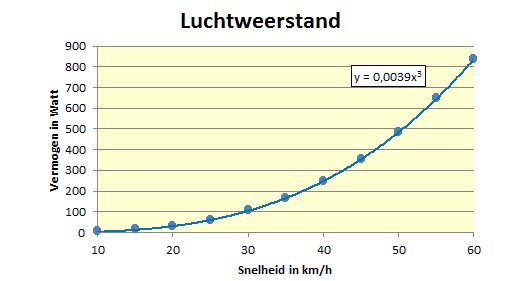
LuchtweerstandHet benodigde vermogen om de luchtweerstand te overwinnen is afhankelijk van de dichtheid van de lucht ρ (in kg/m3 ), de weerstandsfactor cdA, de snelheid v (in m/s) en de windsnelheid vw (in m/s), zoals weergegeven in de box.

Ook hier is het voorbeeld weer voor snelle Eddy, die in dit geval rijdt in tijdrithouding (cdA = 0,3) en bij een temperatuur van 20 °C (hierbij is de dichtheid van de lucht 1,205 kg/m3). Uit het voorbeeld blijkt dat de luchtweerstand het leeuwendeel van zijn beschikbaar vermogen vergt, namelijk 248/300= 83%. Uit de formule en de grafiek blijkt ook dat de luchtweerstand toeneemt met de 3e macht van de snelheid. Om snelheden boven de 40 km/h te bereiken neemt het benodigde vermogen dus enorm toe, tot meer dan 800 Watt bij 60 km/h. We begrijpen nu meteen waarom het onmogelijk is om dergelijke snelheden vol te houden, want de grens van het menselijke duurvermogen ligt bij een ADV van 6,4 Watt/kg x 75 kg = 480 Watt.In deel II gaan we nader in op alle factoren die de luchtweerstand bepalen en het effect daarvan op de haalbare snelheid.
 Klimweerstand
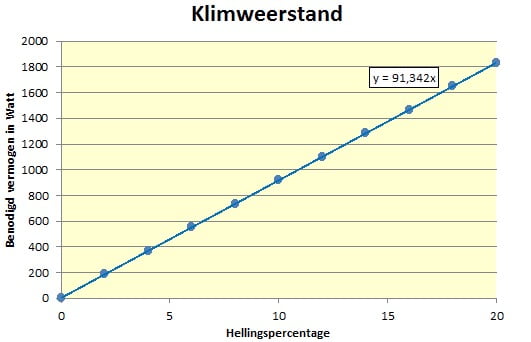
KlimweerstandDe klimweerstand is afhankelijk van het hellingspercentage i (in %), het gewicht m (in kg) en de snelheid v (in m/s), conform de formule in de box.

Het voorbeeld is weer voor snelle Eddy, die in dit geval de Alpe d’Huez probeert te beklimmen. Uit de box is meteen duidelijk dat hij een snelheid van 40 km/h bergop nooit kan volhouden, want dit zou een vermogen vergen van maar liefst 677 Watt, terwijl zijn totale vermogen maar 300 Watt bedraagt. Zoals uit de formule en de onderstaande grafiek (die ook geldt voor 40 km/h) blijkt, neemthet benodigde vermogen bergop enorm toe. Het gevolg is uiteraard bekend: de snelheid neemt zelfs voor de wereldtoppers af tot een tempo dat voetgangers kunnen bijhouden op steile hellingen.In een later artikel gaan we nader in op alle factoren die de klimweerstand bepalen en het effect daarvan op de haalbare snelheid. Voor de volledigheid melden we ook hier nog even dat strikt genomen in de bovenstaande formule nog een factor sin(boogtan(i/100)) moet worden toegevoegd, waarbij i het hellingspercentage is. In de praktijk is deze factor nagenoeg gelijk aan 1 (zelfs bij een helling van 20% is hij maar 0,98). We hebben hem dus in de box maar weggelaten, in onze calculatoren op www.hetgeheimvanwielrennen.nl hebben we hem uiteraard wel meegenomen.
Voor wielrenners die niet in de gelegenheid zijn om in de bergen te trainen, hebben we nog onderstaande grafiek gemaakt, die bijvoorbeeld laat zien dat de benodigde weerstand om een tegenwind van 60 km/h te overwinnen vrijwel gelijk is aan de weerstand op een helling van 5%. Zo is het dus toch mogelijk om bergtraining te doen is ons vlakke landje….
 Mechanische weerstand
Mechanische weerstandDe mechanische weerstand van naven en ketting wordt in het algemeen uitgedrukt als een percentage van het totaal beschikbaar vermogen. Het rendement η van de overbrenging ligt in de orde van 97,5%, zodat het verlies van de mechanische weerstand 2,5% bedraagt. Voor snelle Eddy gaat hiermee dus 0,025*300 = 7,5 Watt verloren. Het is dus zeker de moeite waard om ketting en naven in optimale conditie te houden.In een later artikel gaan we nader in op alle factoren die de mechanische weerstand bepalen en het effect daarvan op de haalbare snelheid.
ConclusiesDe natuurkunde van het fietsen bestaat in wezen uit het formuleren van de vergelijkingen die de 4 weerstanden bepalen. In de evenwichtssituatie moet de som van deze 4 weerstanden gelijk zijn aan het beschikbare vermogen van de wielrenner. Het uiteindelijke resultaat is dus de vrij ingewikkelde 3e graads vergelijking die onderaan in de box is geformuleerd. In een volgend artikel gaan we uitleggen hoe we die ‘wielrenvergelijking’ opgelost hebben en hoe onze calculatoren van www.hetgeheimvanwielrennen.nl gebruikt kunnen worden om uit te rekenen hoe snel je kunt fietsen en wat voor effect de verschillende factoren en omstandigheden daarop hebben.

Je kunt het effect van alle aspecten op je eigen prestaties berekenen met onze calculators op
www.hetgeheimvanwielrennen.nl.Daar kun je ook ons boek bestellen. Het is ook verkrijgbaar als ebook.Hans van Dijk, Ron van Megen en Guido Vroemen
 Het voorbeeld is weer voor snelle Eddy, die 75 kg weegt en een fiets heeft van 8,8 kg. Zijn ADV is 4 Watt/kg, dus in totaal kan hij 4*75 = 300 Watt trappen. Bij een snelheid van 40 km/h is het aandeel van de rolweerstand in zijn totale vermogen dus 36,5/300 = 12,1%. In de grafiek zien we dat de rolweerstand van Snelle Eddy in de praktijk kan variëren van 10-55 Watt.In deel II gaan we nader in op alle factoren die de rolweerstand bepalen en het effect daarvan op de haalbare snelheid.Voor de volledigheid melden we hier nog even dat strikt genomen in de bovenstaande formule nog een factor cos(boogtan(i/100)) moet worden toegevoegd, waarbij i het hellingspercentage is. In de praktijk is deze factor nagenoeg gelijk aan 1 (zelfs bij een helling van 20% is hij maar 0,98). We hebben hem dus in de box maar weggelaten, in onze calculatoren op www.hetgeheimvanwielrennen.nl hebben we hem uiteraard wel meegenomen.
Het voorbeeld is weer voor snelle Eddy, die 75 kg weegt en een fiets heeft van 8,8 kg. Zijn ADV is 4 Watt/kg, dus in totaal kan hij 4*75 = 300 Watt trappen. Bij een snelheid van 40 km/h is het aandeel van de rolweerstand in zijn totale vermogen dus 36,5/300 = 12,1%. In de grafiek zien we dat de rolweerstand van Snelle Eddy in de praktijk kan variëren van 10-55 Watt.In deel II gaan we nader in op alle factoren die de rolweerstand bepalen en het effect daarvan op de haalbare snelheid.Voor de volledigheid melden we hier nog even dat strikt genomen in de bovenstaande formule nog een factor cos(boogtan(i/100)) moet worden toegevoegd, waarbij i het hellingspercentage is. In de praktijk is deze factor nagenoeg gelijk aan 1 (zelfs bij een helling van 20% is hij maar 0,98). We hebben hem dus in de box maar weggelaten, in onze calculatoren op www.hetgeheimvanwielrennen.nl hebben we hem uiteraard wel meegenomen. LuchtweerstandHet benodigde vermogen om de luchtweerstand te overwinnen is afhankelijk van de dichtheid van de lucht ρ (in kg/m3 ), de weerstandsfactor cdA, de snelheid v (in m/s) en de windsnelheid vw (in m/s), zoals weergegeven in de box.
LuchtweerstandHet benodigde vermogen om de luchtweerstand te overwinnen is afhankelijk van de dichtheid van de lucht ρ (in kg/m3 ), de weerstandsfactor cdA, de snelheid v (in m/s) en de windsnelheid vw (in m/s), zoals weergegeven in de box. Ook hier is het voorbeeld weer voor snelle Eddy, die in dit geval rijdt in tijdrithouding (cdA = 0,3) en bij een temperatuur van 20 °C (hierbij is de dichtheid van de lucht 1,205 kg/m3). Uit het voorbeeld blijkt dat de luchtweerstand het leeuwendeel van zijn beschikbaar vermogen vergt, namelijk 248/300= 83%. Uit de formule en de grafiek blijkt ook dat de luchtweerstand toeneemt met de 3e macht van de snelheid. Om snelheden boven de 40 km/h te bereiken neemt het benodigde vermogen dus enorm toe, tot meer dan 800 Watt bij 60 km/h. We begrijpen nu meteen waarom het onmogelijk is om dergelijke snelheden vol te houden, want de grens van het menselijke duurvermogen ligt bij een ADV van 6,4 Watt/kg x 75 kg = 480 Watt.In deel II gaan we nader in op alle factoren die de luchtweerstand bepalen en het effect daarvan op de haalbare snelheid.
Ook hier is het voorbeeld weer voor snelle Eddy, die in dit geval rijdt in tijdrithouding (cdA = 0,3) en bij een temperatuur van 20 °C (hierbij is de dichtheid van de lucht 1,205 kg/m3). Uit het voorbeeld blijkt dat de luchtweerstand het leeuwendeel van zijn beschikbaar vermogen vergt, namelijk 248/300= 83%. Uit de formule en de grafiek blijkt ook dat de luchtweerstand toeneemt met de 3e macht van de snelheid. Om snelheden boven de 40 km/h te bereiken neemt het benodigde vermogen dus enorm toe, tot meer dan 800 Watt bij 60 km/h. We begrijpen nu meteen waarom het onmogelijk is om dergelijke snelheden vol te houden, want de grens van het menselijke duurvermogen ligt bij een ADV van 6,4 Watt/kg x 75 kg = 480 Watt.In deel II gaan we nader in op alle factoren die de luchtweerstand bepalen en het effect daarvan op de haalbare snelheid. KlimweerstandDe klimweerstand is afhankelijk van het hellingspercentage i (in %), het gewicht m (in kg) en de snelheid v (in m/s), conform de formule in de box.
KlimweerstandDe klimweerstand is afhankelijk van het hellingspercentage i (in %), het gewicht m (in kg) en de snelheid v (in m/s), conform de formule in de box. Het voorbeeld is weer voor snelle Eddy, die in dit geval de Alpe d’Huez probeert te beklimmen. Uit de box is meteen duidelijk dat hij een snelheid van 40 km/h bergop nooit kan volhouden, want dit zou een vermogen vergen van maar liefst 677 Watt, terwijl zijn totale vermogen maar 300 Watt bedraagt. Zoals uit de formule en de onderstaande grafiek (die ook geldt voor 40 km/h) blijkt, neemthet benodigde vermogen bergop enorm toe. Het gevolg is uiteraard bekend: de snelheid neemt zelfs voor de wereldtoppers af tot een tempo dat voetgangers kunnen bijhouden op steile hellingen.In een later artikel gaan we nader in op alle factoren die de klimweerstand bepalen en het effect daarvan op de haalbare snelheid. Voor de volledigheid melden we ook hier nog even dat strikt genomen in de bovenstaande formule nog een factor sin(boogtan(i/100)) moet worden toegevoegd, waarbij i het hellingspercentage is. In de praktijk is deze factor nagenoeg gelijk aan 1 (zelfs bij een helling van 20% is hij maar 0,98). We hebben hem dus in de box maar weggelaten, in onze calculatoren op www.hetgeheimvanwielrennen.nl hebben we hem uiteraard wel meegenomen.
Het voorbeeld is weer voor snelle Eddy, die in dit geval de Alpe d’Huez probeert te beklimmen. Uit de box is meteen duidelijk dat hij een snelheid van 40 km/h bergop nooit kan volhouden, want dit zou een vermogen vergen van maar liefst 677 Watt, terwijl zijn totale vermogen maar 300 Watt bedraagt. Zoals uit de formule en de onderstaande grafiek (die ook geldt voor 40 km/h) blijkt, neemthet benodigde vermogen bergop enorm toe. Het gevolg is uiteraard bekend: de snelheid neemt zelfs voor de wereldtoppers af tot een tempo dat voetgangers kunnen bijhouden op steile hellingen.In een later artikel gaan we nader in op alle factoren die de klimweerstand bepalen en het effect daarvan op de haalbare snelheid. Voor de volledigheid melden we ook hier nog even dat strikt genomen in de bovenstaande formule nog een factor sin(boogtan(i/100)) moet worden toegevoegd, waarbij i het hellingspercentage is. In de praktijk is deze factor nagenoeg gelijk aan 1 (zelfs bij een helling van 20% is hij maar 0,98). We hebben hem dus in de box maar weggelaten, in onze calculatoren op www.hetgeheimvanwielrennen.nl hebben we hem uiteraard wel meegenomen. Voor wielrenners die niet in de gelegenheid zijn om in de bergen te trainen, hebben we nog onderstaande grafiek gemaakt, die bijvoorbeeld laat zien dat de benodigde weerstand om een tegenwind van 60 km/h te overwinnen vrijwel gelijk is aan de weerstand op een helling van 5%. Zo is het dus toch mogelijk om bergtraining te doen is ons vlakke landje….
Voor wielrenners die niet in de gelegenheid zijn om in de bergen te trainen, hebben we nog onderstaande grafiek gemaakt, die bijvoorbeeld laat zien dat de benodigde weerstand om een tegenwind van 60 km/h te overwinnen vrijwel gelijk is aan de weerstand op een helling van 5%. Zo is het dus toch mogelijk om bergtraining te doen is ons vlakke landje…. Mechanische weerstandDe mechanische weerstand van naven en ketting wordt in het algemeen uitgedrukt als een percentage van het totaal beschikbaar vermogen. Het rendement η van de overbrenging ligt in de orde van 97,5%, zodat het verlies van de mechanische weerstand 2,5% bedraagt. Voor snelle Eddy gaat hiermee dus 0,025*300 = 7,5 Watt verloren. Het is dus zeker de moeite waard om ketting en naven in optimale conditie te houden.In een later artikel gaan we nader in op alle factoren die de mechanische weerstand bepalen en het effect daarvan op de haalbare snelheid.ConclusiesDe natuurkunde van het fietsen bestaat in wezen uit het formuleren van de vergelijkingen die de 4 weerstanden bepalen. In de evenwichtssituatie moet de som van deze 4 weerstanden gelijk zijn aan het beschikbare vermogen van de wielrenner. Het uiteindelijke resultaat is dus de vrij ingewikkelde 3e graads vergelijking die onderaan in de box is geformuleerd. In een volgend artikel gaan we uitleggen hoe we die ‘wielrenvergelijking’ opgelost hebben en hoe onze calculatoren van www.hetgeheimvanwielrennen.nl gebruikt kunnen worden om uit te rekenen hoe snel je kunt fietsen en wat voor effect de verschillende factoren en omstandigheden daarop hebben.
Mechanische weerstandDe mechanische weerstand van naven en ketting wordt in het algemeen uitgedrukt als een percentage van het totaal beschikbaar vermogen. Het rendement η van de overbrenging ligt in de orde van 97,5%, zodat het verlies van de mechanische weerstand 2,5% bedraagt. Voor snelle Eddy gaat hiermee dus 0,025*300 = 7,5 Watt verloren. Het is dus zeker de moeite waard om ketting en naven in optimale conditie te houden.In een later artikel gaan we nader in op alle factoren die de mechanische weerstand bepalen en het effect daarvan op de haalbare snelheid.ConclusiesDe natuurkunde van het fietsen bestaat in wezen uit het formuleren van de vergelijkingen die de 4 weerstanden bepalen. In de evenwichtssituatie moet de som van deze 4 weerstanden gelijk zijn aan het beschikbare vermogen van de wielrenner. Het uiteindelijke resultaat is dus de vrij ingewikkelde 3e graads vergelijking die onderaan in de box is geformuleerd. In een volgend artikel gaan we uitleggen hoe we die ‘wielrenvergelijking’ opgelost hebben en hoe onze calculatoren van www.hetgeheimvanwielrennen.nl gebruikt kunnen worden om uit te rekenen hoe snel je kunt fietsen en wat voor effect de verschillende factoren en omstandigheden daarop hebben. Je kunt het effect van alle aspecten op je eigen prestaties berekenen met onze calculators op www.hetgeheimvanwielrennen.nl.Daar kun je ook ons boek bestellen. Het is ook verkrijgbaar als ebook.Hans van Dijk, Ron van Megen en Guido Vroemen
Je kunt het effect van alle aspecten op je eigen prestaties berekenen met onze calculators op www.hetgeheimvanwielrennen.nl.Daar kun je ook ons boek bestellen. Het is ook verkrijgbaar als ebook.Hans van Dijk, Ron van Megen en Guido Vroemen

